Les différentes images du jour
-
-
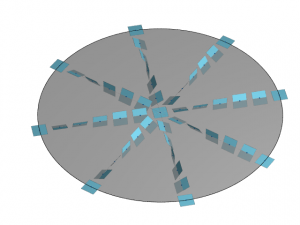
Feuilletage caractéristique de la sphère $S^2$, par...Voir l'image -
-
Feuilletage caractéristique de la sphère $S^2$, par...Voir l'image -
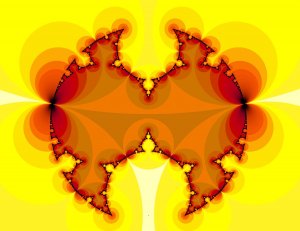
Méthode de tracé d’ensembles de Julia transcendant mettant en valeur sa structure feuilletée.Voir l'image -
-
-
-
Prenez un crayon et dessinez une courbe qui se referme sur une feuille de papier, un cercle par exemple. Si vous découpez la feuille avec des ciseaux le long de la courbe, vous obtenez deux...Voir l'image -
Qu’est-ce qu’une courbe ? Au fil des siècles, les mathématiciens ont diversifié leurs points de vue sur les courbes. Les grecs anciens ont considéré les droites, les cercles,...Voir l'image -
Une courbe fermée qui ne se recoupe pas décompose le plan en deux composantes : c’est le théorème de Jordan. Un théorème important a été énoncé par Osgood en 1902 mais la...Voir l'image -
Tracez une courbe fermée dans l’espace, sans passer deux fois par le même point. Vous obtenez ce qu’on appelle un nœud. Il y a beaucoup de façons de faire des nœuds ! On dit que...Voir l'image -
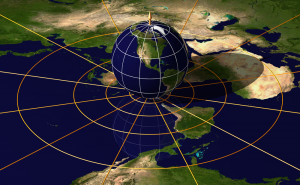
Pourquoi dit-on que la Terre est une sphère est de dimension 2 ? Parce que ses habitants (nous !) vivent à sa surface. Pour se repérer et indiquer une position sur Terre, il nous faut...Voir l'image -
Pendant longtemps, la géométrie algébrique s’est préoccupée des "courbes algébriques". Il s’agit de courbes dans le plan qui sont définies par une équation, comme par exemple...Voir l'image -
Dès que l’on pense à chacune des deux coordonnées d’un plan comme un nombre complexe, chacun possédant une partie réelle et une partie imaginaire, le plan complexe devient de...Voir l'image -
Le cercle de rayon 1 dans le plan est le cercle trigonométrique ; celui où on repère sa position par un angle. Une propriété très importante est qu’on peut ajouter deux angles pour...Voir l'image -
En 1963, le météorologiste E. Lorenz étudie le mouvement de l’atmosphère. Mathématiquement, le problème est extrêmement compliqué. Pour décrire la situation à un instant donné, il...Voir l'image -
Dans les années 1960, les mathématiciens comprennent que certains mouvements peuvent être à la fois "chaotiques" et "stables", ce qui semble pourtant contradictoire... Le chaos fait référence...Voir l'image -
Chaque ligne et chaque colonne contiennent un unique "grand" carré de chaque couleur, un unique "petit" carré de chaque couleur. Aucun couple de couleurs "grand carré/petit carré"...Voir l'image -
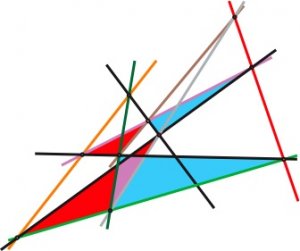
Sur cette figure, il y a dix droites, et sur ces droites, dix points sont marqués de façon que chacune des droites contient trois des points, chacun des points est sur trois des droites.Voir l'image
