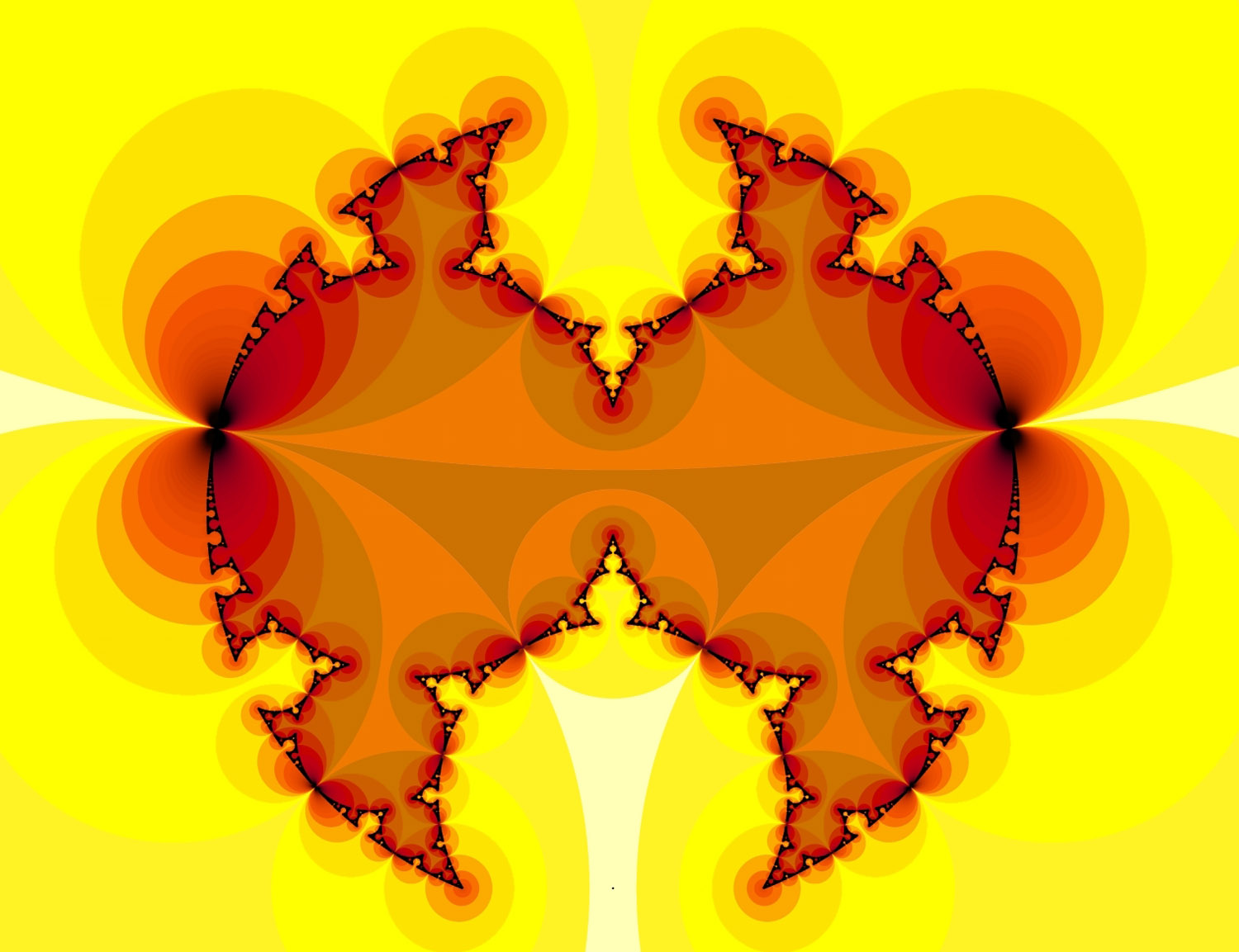
Prenez un crayon et dessinez une courbe qui se referme sur une feuille de papier, un cercle par exemple. Si vous découpez la feuille avec des ciseaux le long de la courbe, vous obtenez deux morceaux : l’intérieur et l’extérieur de la courbe. Bien sûr, si la courbe se recoupe — comme lorsqu’on écrit un 8 par exemple — la découpe peut produire trois morceaux, ou plus. Le théorème de Jordan affirme qu’une courbe fermée continue qui ne passe pas deux fois au même endroit, découpe le plan en exactement deux morceaux.

Evident ? Vers la fin du dix-neuvième siècle, les courbes continues au comportement très irrégulier font leur apparition en mathématiques : le besoin d’une preuve de cette "évidence" se fait sentir. Jordan "démontre son théorème" en 1887 mais sa "preuve" ne convaincra pas ses collègues... Il faudra attendre une preuve en 1905 par Veblen pour que tout le monde soit convaincu ! La figure représente l’une de ces "courbes de Jordan". Partant d’un chapelet de quatre disques tangents, on construit successivement, par des inversions successives, des chapelets de disques tangents qui sont constitués de plus en plus de disques, de plus en plus petits. La limite des chapelets est une courbe fermée et continue, qui a donc un intérieur et un extérieur d’après Jordan.