L'image du Décembre 2024

Un nœud et sa surface de Seifert

Un nœud et sa surface de Seifert

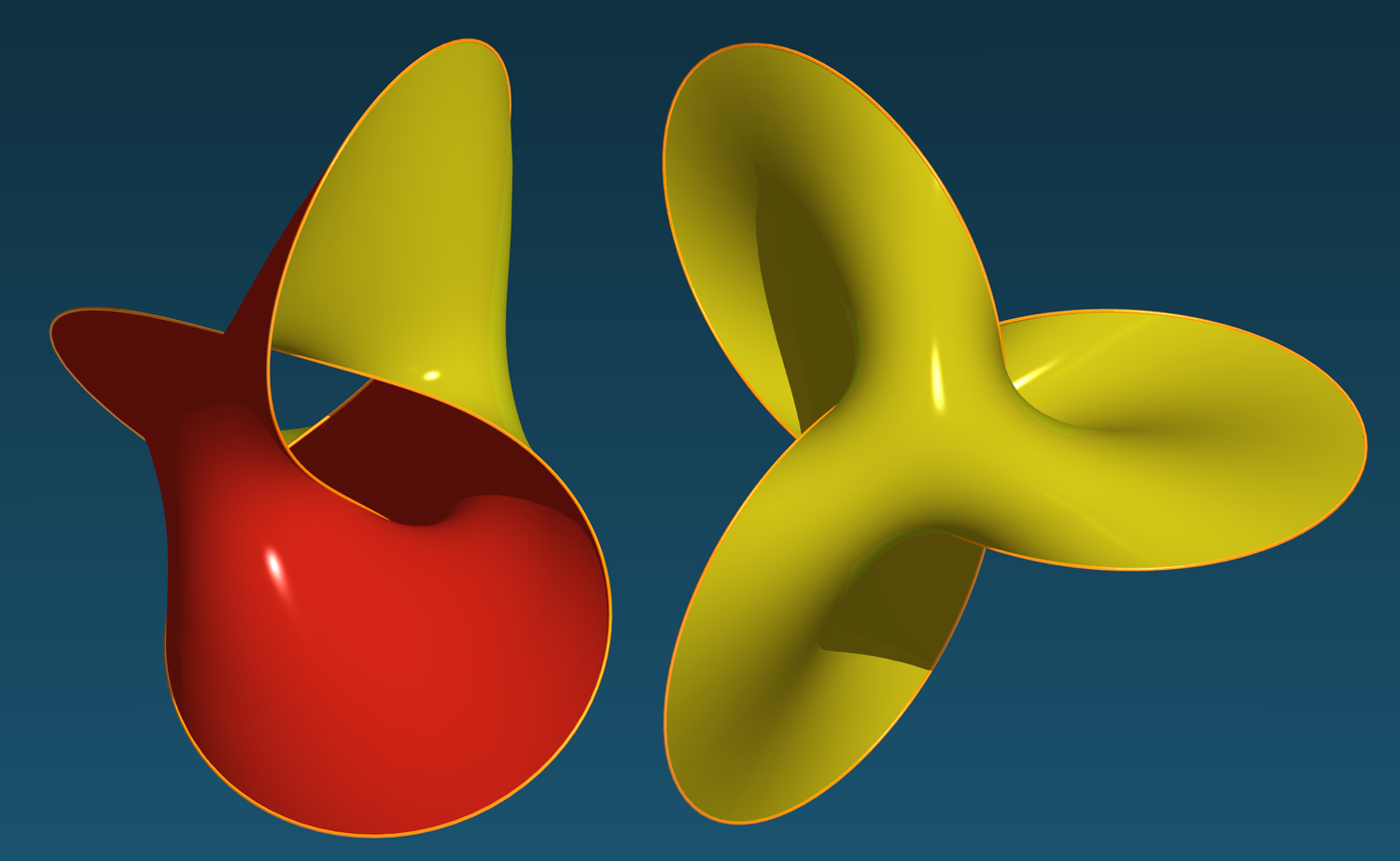
Tracez une courbe fermée dans l’espace, sans passer deux fois par le même point. Vous obtenez ce qu’on appelle un nœud. Il y a beaucoup de façons de faire des nœuds ! On dit que deux nœuds sont "les mêmes" ("isotopes" en termes techniques) si on peut déformer continûment le premier pour le transformer en l’autre sans introduire de points d’intersection. Le but de la théorie des nœuds serait de déterminer tous les nœuds... Des tables de nœuds existent mais elles n’épuisent pas toutes les possibilités, qui sont en nombre infini. L’un des fondateurs de la théorie, Seifert, a introduit un outil remarquable pour étudier les nœuds : les surfaces de Seifert. Un nœud est une courbe, donc de dimension 1 ; il est situé dans l’espace de dimension 3 et le théorème de Seifert affirme qu’il est toujours possible de trouver une surface, donc de dimension 2, située dans l’espace, dont le bord est le nœud étudié. Ici, on montre deux vues d’un nœud très simple, le nœud de trèfle (celui utilisé par beaucoup d’entre nous pour leurs lacets de chaussures) et une surface de Seifert. Les deux faces de la surface sont coloriées en jaune et en rouge.


Voir d'autres images du jour.

Ressources pédagogiques

Actualités des maths