L'image du Août 2024

Illustration de la conjecture de Goldbach, par Jean-François Colonna.

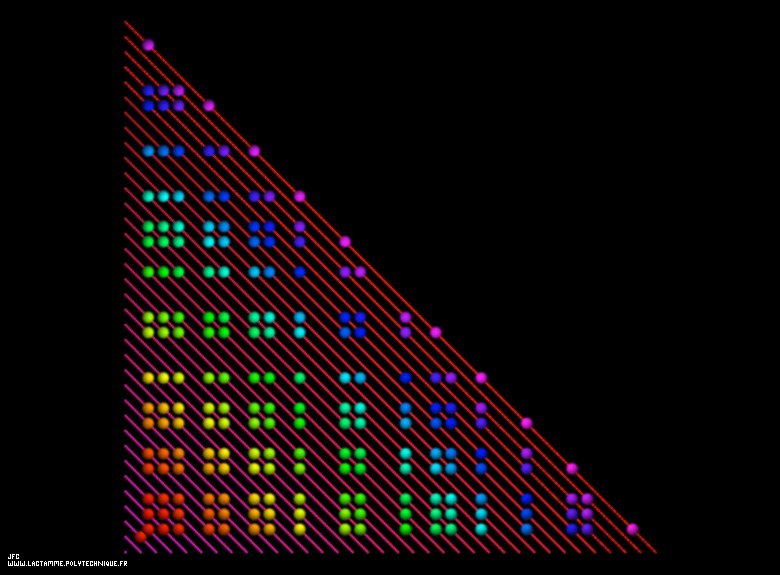
Illustration de la conjecture de Goldbach, par Jean-François Colonna.

Chaque segment d’équation $Y=-X+N$ représente un nombre entier pair
N (à partir de 0, même si la conjecture de Golbach porte sur les
nombres pairs supérieurs ou égaux à 4). Chaque disque matérialise un
couple $P1,P2$ de nombre premiers tel que $N=P1+P2,$ la disque $P2,P1$
étant lui-aussi visualisé.
Chaque
petit disque a pour coordonnées entières P1 et P2, P1 et P2 étant deux
nombres premiers. La Conjecture de Goldbach affirme donc que sur chacune
des lignes il y a au moins un tel disque.

Crédits : Jean-François Colonna http://www.lactamme.polytechnique.fr/Mosaic/images/GOLD.11.D/display.html


Voir d'autres images du jour.

Ressources pédagogiques

Actualités des maths